|
Propeller Head Plaza Technical and scientific discussion of amps, cables and other topics. |
|
|
|
Propeller Head Plaza Technical and scientific discussion of amps, cables and other topics. |
|
In Reply to: Let's see what you don't understand, then... posted by real_jj on June 16, 2006 at 12:24:11:
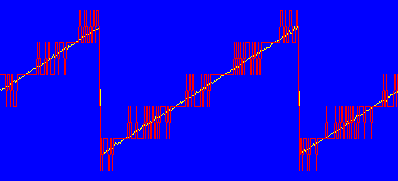
One who's dogmatic about misinformation being truth will interpret truth as misinformation....Let's go to Page 10.... It states:
Features of a HP filter
At the frequency where the amplitude is greatest, the phase is changing rapidly.
This is only true if there is a resonance between the passband and the stopband. (Which happens to be the case in the graphic example.) Otherwise, the opposite is true- The phase changes slowly where the amplitude is greatest.
The statement more accurately would be: "At the frequency where the *transition* in amplitude is greatest, the phase changes rapidly."
On Page 32....
A reminder about Duality in the Fourier domain
• Multiplying two signals means that you convolve their (full, complex) spectra.
• Convolving two signals means that you multiply their (full, complex) spectra.The above statements are not the basic Fourier duality.... And convolution is *not* applied to spectra in audio DSP. It's only applied to signals in the *time* domain. For a more detailed explanation, click here...
The basic duality in Fourier analysis deals with time domain and frequency domain. The "Fourier transform" depicts the relationship (or "duality") of periodic signals between the time domain (the waveform) and frequency domain (frequency response).
Now convolution in the time domain equates to multiplication in the frequency domain.... The "brickwall" filter, used in digital audio filters, is multiplied with the spectrum of the original signal.
On Page 34....
• That means that we CONVOLVE the signal spectrum and the sampling spectrum.
Once again, the **spectrum** is not what's convolved. Until the signal itself is filtered to prevent out-of-band aliasing, no convolution takes place.
- Hence, we have the Nyquist criterion, later proven by Shannon.
The criterion exists, but not based on the above text. It exists because it's physically impossible to reconstruct signals at and above Fs/2.
On Page 45....
dither RAISES the noise floor, and lowers the PERCIEVED noise floor.
It is presumed that a DBT study has taken place to substantiate this.... Otherwise it's a subjective opinion stated as fact.
On Page 46....
Quantization requires TPD.
The type of dither applied that is most-ideal has never been unanimously agreed-upon.
On Page 47....
What about reconstruction?
Yes, that convolution theorem applies again, this time usually convolving a “square pulse†with the digital signal.
While the effect of non-filtered playback is similar to "convolving with a square pulse," no such mathematical computation actually takes place. It's a natural phenomenon in non-filtered playback.
• This leads to a form of signal “imagesâ€. While “images†and “aliases†come about by mathematically similar processes, people persist in having different names for them.
• Some (many in the high end) omit the anti-imaging filter, and imagine that there is a ‘beating’ problem. If you haven’t heard this yet, you will at some point. The next few graphs show why it isn’t so.When no filtering is applied, beating indeed exists.... Click here (Diagrams 12 and 13) for a depiction of it....
Page 51....
In reconstruction, filtering is also necessary to remove the “image†signals that originate in the same fashion as aliases arise in sampling.
In the case of sampling, filtering is necessary to prevent images of out-of-band signals from potentially occurring in band (and stored on the media, which cannot be removed). In the case of re-construction, filtering prevents images in-band from occurring out-of-band. Designers of "non-OS" DACs think the latter case is **not** necessary. Since the ill effects occur outside the spectrum of human hearing.
• In reconstruction, the waveform is sometimes a “step†rather than an impulse, so other compensation is sometimes necessary to get a flat frequency response. Why?
• Again, using the “step†in time (convolving) means that you multiply the signal by the frequency response of the “step†in the frequency domain, leading to a rolloff like sin(x)/x.The "step" function in the time domain is in actually the *brickwall* filter in the frequency domain.... Using the "Fourier transform" of the brickwall function, which happens to be "sin(x)/x" AKA the "sinc" function (not the "step" function), in the *time* domain. The raw digital waveform is convolved, in real time, with a "windowed" version of this "sinc" function. The resultant signal has a flat response to near Fs/2, with virtually no beating.
Modern convertors of the delta-sigma variety do not use a step at the final sampling frequency (although they certainly use a “step†it’s at a much higher frequency). Their design, however, introduces other issues. That discussion comes later.
Delta-sigma converters use an intermediate process where the DSP signal is converted to a pulse train, then converted to analog via pulse-density or pulse-width modulation. Unless specified otherwise, they use "brickwall" filters too. Using a brickwall filter (or what is called "step" in the doc) at a higher frequency will introduce the near out of band aliases cited earlier.
The graph on Page 54 suggests that the pre-digitized and quantized/dithered signals are identical. They may be for large signals, but at levels of less than 10 times the LSB, they can be very different. See graphic here on how they can be different.
On Page 55....
It’s really hard to see quantization at even very noisy levels in a waveform plot.
It's not hard to see it in the graphic.... It's a presumption based on a single graphic plot that happens to not show a difference. But it wrongly presumes such differences never exist.
• NOTICE THAT NOISE SPREADS OVER THE ENTIRE OUTPUT SPECTRUM.
Why the caps? What's the point?
(The graph on Page 57 does not really show anything....)
Page 58....
That demonstrates the most trivial form of oversampling.
This trivial form of oversampling provides the equivalent of 1 bit, in-band, for every 4x the sampling frequency, i.e. 3db per doubling
Oversampling is how a digital filter is implemented. It has nothing to do with improving signal-to-noise ratio.....
Page 61....
Like many graphs in the doc, there are no units or descriptions on the X or Y axes.... What is being depicted here? (This is what one of my professors in college would call "handwaving"....)
Page 62....
• Within limits, using a noise-shaping system, you can move the noise around in frequency.
• You can, for instance, push lots of the noise up to high frequencies.
• That is one of the reasons for oversampling.Oversampling has no impact on noise shaping. It's a form of digital filtering.
Page 63....
What’s another reason for Oversampling?
You get to control the response of the initial anti-aliasing/anti-imaging filter digitally.That is the real reason for oversampling.... And the *sole* reason for oversampling!!!
Page 66....
• The 13th order analog filter (with horrible phase response) is replaced by a 5th order analog filter.
The "orders" of the filters can vary greatly with A/D utilized.... And a 5th order analog filter also has "horrible phase response".... Many A/D use a purely "digital" filter at Fs/2, with a gradual analog filter at a higher frequency. (This would eliminate the "horrible phase response.") Just like in the D/A process. Except it's an analog "pre" filter instead of a "post" filter.
Page 73....
Downsample by zeroing 3 of every 4 samples and multiplying the others by 4.
This would mangle the signal. You basically have pulses every fourth sample. (Whether these pulses are "multiplied by 4" doesn't make any difference. Except that the signal may end up being "clipped.")
Page 75....
Massive oversampling:
• Remember: One gets 3dB per doubling of Fs from oversampling with a flat noise floor.
• If we also put a single integrator with its zero at 20kHz into H(s), we will see that the increased SNR available is 3 + 6 db/doubling of Fs. There will be some cost in the form of a constant negative term to this SNR, which is overcome by very moderate levels of oversampling.If this were the case, 65,536x oversampling should have **incredible** S/N ratio....
"Very moderate levels of oversampling".... Can this be quantified and fine-tuned?
Page 77....
• Remember, nearly the same amount of noise is being shaped in each case.
• As there is more “space†under the curve at high frequencies, more of the noise moves to high frequencies.
• That means there is LESS noise at low frequencies.And more noise at high frequencies, which I say is not necessarily a good thing....
• Therefore, if we FILTER OUT the high frequencies, we wind up with a lower sampling rate signal with a higher SNR.
If this is implying noise can be pushed up above Fs/2 and then filtered out, it's wishful thinking... You'd basically be *removing* dither.... For once again, the (anti-aliasing) filtering occurs *before* quantization.
Well, there you have it....
This post is made possible by the generous support of people like you and our sponsors:
Follow Ups
- Re: Let's see what you don't understand, then... - Todd Krieger 23:36:20 06/16/06 (5)
- Incredible, you're zero for all! - real_jj 00:09:22 06/17/06 (4)
- A Word of Advice..... - Todd Krieger 00:36:39 06/17/06 (3)
- Get lost, you miseducating stalker. - real_jj 00:52:46 06/17/06 (2)
- If Your Head Got Any Bigger.... - Todd Krieger 01:00:54 06/17/06 (1)
- Go back to www.timecube.com, Todd - real_jj 01:16:18 06/17/06 (0)
Top of Page ]
[ Contact Us ]
[ Support/Wish List ]
[ Copyright © 2025, Audio Asylum, all rights reserved ]
